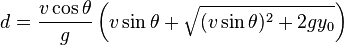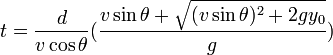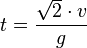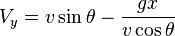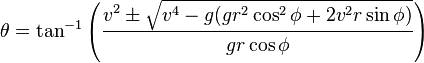Trajectory of a projectile

From Wikipedia, the free encyclopedia

The United States Department of Defense, and NATO define a ballistic trajectory as a trajectory traced after the propulsive force is terminated and the body is acted upon only by gravity and aerodynamic drag.^[1]

[edit] Notation

In the equations on this page, the following variables will be used:

g: the gravitational acceleration—usually taken to be 9.81 m/s² near the Earth's surface
θ: the angle at which the projectile is launched
v: the velocity at which the projectile is launched
y₀: the initial height of the projectile
d: the total horizontal distance traveled by the projectile

[edit] Conditions at the final position of the projectile

[edit] Distance travelled

The total horizontal distance (d) traveled.

$d = \frac{v \cos \theta}{g} \left( v \sin \theta + \sqrt{(v \sin \theta)^2 + 2gy_0} \right)$

When the surface the object is launched from and is flying over is flat, the distance traveled is:

$d = \frac{v^2 \sin(2 \theta)}{g}$

As a special case, the distance is given by

$d = \frac{v^2}{g}$

when the angle (θ) is 45° and the initial height (y₀) is 0.

For explicit derivations of these results, see Range of a projectile.

[edit] Time of flight

The time of flight (t) is the time it takes for the projectile to finish its trajectory.

$t = \frac{d}{v \cos\theta} ( \frac{v \sin \theta + \sqrt{(v \sin \theta)^2 + 2gy_0}}{g})$

As above, this expression can be reduced to

$t = \frac{\sqrt{2} \cdot v}{g}$

if θ is 45° and y₀ is 0.

The above results are found in Range of a projectile.

`[edit] Angle of reach`

The "angle of reach" (not quite a scientific term) is the angle (θ) at which a projectile must be launched in order to go a distance d, given the initial velocity v.

$\sin(2\theta) = \frac{gd}{v^2}$

$\theta = \frac{1}{2} \arcsin \left( \frac{gd}{v^2} \right)$

[edit] Conditions at an arbitrary distance `x`

[edit] Height at `x`

The height y of the projectile at distance x is given by

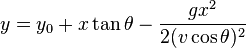$y = y_0 + x \tan \theta - \frac {gx^2}{2(v\cos\theta)^2}$ .

The second term is the deviation from traveling in a straight line.

[edit] Velocity at `x`

The magnitude, $| v | ,$ of the velocity of the projectile at distance x is given by

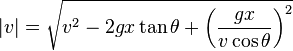$| v | = \sqrt{v^2 - 2gx \tan \theta + \left(\frac{gx}{v\cos \theta}\right)^2}$ .

[edit] Derivation

The magnitude |v| of the velocity is given by

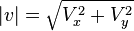$| v | = \sqrt{V_x^2 + V_y^2}$ ,

where V_x and V_y are the instantaneous velocities in the x- and y-directions, respectively.

Here the x-velocity remains constant; it is always equal to v cos θ.

The y-velocity can be found using the formula

v f = v i + a t

by setting v_i = v sin θ, a = g, and 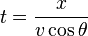$t = \frac{x}{v \cos \theta}$ . (The latter is found by taking x = (v cos θ) t and solving for t.) Then,

$V_y = v \sin \theta - \frac{gx}{v \cos \theta}$

and

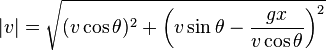$| v | = \sqrt{(v \cos \theta)^2 + \left(v \sin \theta - \frac{gx}{v \cos \theta} \right)^2}$ .

The formula above is found by simplifying.

[edit] Angle $θ$ required to hit coordinate (`x`,`y`)

To hit a target at range x and altitude y when fired from (0,0) and with initial velocity v the required angle(s) of launch $θ$ are:

$\theta = \tan^{-1}{\left(\frac{v^2\pm\sqrt{v^4-g(gx^2+2yv^2)}}{gx}\right)}$

Each root of the equation corresponds to the two possible launch angles so long as both roots aren't imaginary, in which case the initial velocity is not great enough to reach the point (x,y) you have selected. The greatest feature of this formula is that it allows you to find the angle of launch needed without the restriction of y = 0.

Derivation

First, two elementary formulae are called upon relating to projectile motion:

$x = v t \cos \theta , t = \frac{x}{v \cos \theta}$ (1)

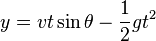$y = vt \sin \theta - \frac{1}{2} g t^2$ (2)

Solving (1) for t and substituting this expression in (2) gives:

$y = x \tan \theta - \frac{gx^2}{2v^2 \cos^2 \theta}$ (2a)

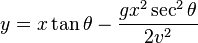$y = x \tan \theta - \frac{gx^2 \sec^2 \theta}{2v^2}$ (2b) (Trigonometric identity)

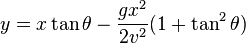$y =x \tan \theta - \frac{gx^2}{2v^2}(1+ \tan^2 \theta)$ (2c) (Trigonometric identity)

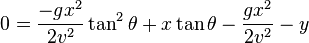$0 = \frac{-gx^2}{2v^2} \tan^2 \theta + x \tan \theta - \frac{gx^2}{2v^2} - y$ (2d) (Algebra)

Let $p = tanθ$

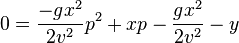$0 = \frac{-gx^2}{2v^2} p^2 + xp - \frac{gx^2}{2v^2} - y$ (2e) (Substitution)

$p = {\frac{-x\pm\sqrt{x^2-4(\frac{-gx^2}{2v^2})(\frac{-gx^2}{2v^2}-y)}}{2(\frac{-gx^2}{2v^2}) }}$ (2f) (Quadratic formula)

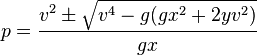$p = \frac{v^2\pm\sqrt{v^4-g(gx^2+2yv^2)}}{gx}$ (2f) (Algebra)

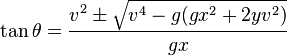$\tan \theta = \frac{v^2\pm\sqrt{v^4-g(gx^2+2yv^2)}}{gx}$ (2g) (Substitution)

$\theta = \tan^{-1}{\left(\frac{v^2\pm\sqrt{v^4-g(gx^2+2yv^2)}}{gx}\right)}$ (2h) (Algebra)

Also, if instead of a coordinate (x,y) you're interested in hitting a target at distance r and angle of elevation $φ$ (polar coordinates), use the relationships $x = r cosφ$ and $y = r sinφ$ and substitute to get:

$\theta = \tan^{-1}{\left(\frac{v^2\pm\sqrt{v^4-g(gr^2\cos^2\phi+2v^2r\sin\phi )}}{gr\cos\phi}\right)}$

[edit] Trajectory of a projectile with air resistance

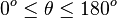Air resistance may be taken to be in direct proportion to the velocity of the particle (i.e. $F_a \propto \vec{v}$ ). Also, $v 0$ , $v x$ and $v y$ will be used to denote the initial velocity, the velocity along the direction of x and the velocity along the direction of y, respectively. The mass of the projectile will be denoted by m. For the derivation only the case where $0^o \le \theta \le 180^o$ is considered. Again, the projectile is fired from the origin (0,0).

For this assumption, the force that air resistance may be taken to be in direct proportion to the velocity of the particle is not correct for a typical projectile in air with a velocity above a few tens of meters/second, and so this equation should not be applied to that situation.

The above free body diagram (not to scale) for a projectile that experiences air resistance and the effects of gravity (the dashed vectors are the x and y components of velocity and air resistance). Here, air resistance is assumed to be in the direction opposite of the projectile's velocity. $F a i r = - k v$ is written due to the initial assumption of direct proportionality implies that the air resistance and the velocity differ only by a constant arbitrary factor, and that when v is increased by a factor of, say, p, the air resistance increases by a factor of p also. As an example, say that when the velocity of the projectile is 4 m/s, the air resistance is 7 newtons (N). When the velocity is doubled to 8 m/s, the air resistance doubles to 14 N accordingly. In this case, k = 7/4 N x s/m. Note that k is needed in order to relate the air resistance and the velocity by an equal sign: otherwise, it would be stating incorrectly that the two are always equal in value (i.e. 1 m/s of velocity gives 1 N of force, 2 m/s gives 2 N etc.) which isn't always the case, and also it keeps the equation dimensionally correct (a force and a velocity cannot be equal to each other, e.g. m/s = N). As another quick example, Hooke's law ( $F = - k x$ ) describes the force produced by a spring when stretched a distance x from its resting position, and is another example of a direct proportion: k in this case has units N/m (in metric).

To show why k = 7/4 N·s/m above, first equate 4 m/s and 7 N:

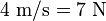$4 \ \mathrm{m}/\mathrm{s} = 7 \ \mathrm{N}$ (Incorrect)

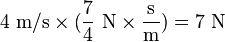$4 \ \mathrm{m}/\mathrm{s} \times (\frac{7}{4} \ \mathrm{N} \times \frac {\mathrm{s}}{\mathrm{m}})= 7 \ \mathrm{N}$ (Introduction of k)

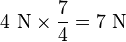$4 \ \mathrm{N} \times \frac{7}{4}= 7 \ \mathrm{N}$ ( $\frac{\mathrm{s}}{\mathrm{m}} \times \frac{\mathrm{m}}{\mathrm{s}}$ cancels)

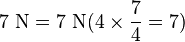
$7 \ \mathrm{N} = 7 \ \mathrm{N} (4 \times \frac{7}{4} = 7)$

For more on proportionality, see: Proportionality (mathematics)

To derive relationships to represent the motion of the particle, Newton's Second Law is first applied ( $Σ F = m a$ ) for both the x and y components:

$m \frac{dv_x}{dt}(=a_x)= -kv_x$ (1)

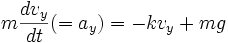$m \frac{dv_y}{dt}(=a_y) = -kv_y+mg$ (2) (The mg term is positive because the value of g is already negative and subtracting it would result in a positive number.)

Note that acceleration is just the derivative of velocity with respect to time ( $a = \frac{dv}{dt}$ ). Solving (1) is an elementary problem in solving differential equations and the solution for $v x$ and, subsequently, x will not be given proof. For initial conditions $v x$ = $v 0 cosθ$ and $x = 0$ for $t = 0$ , these solutions are:

$v_x = v_0 e^{-\frac{kt}{m}}\cos \theta$ (1a)

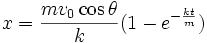$x = \frac{mv_0\cos\theta}{k}(1-e^{-\frac{kt}{m}})$ (1b)

(2) will be solved here for interest. In fact, (1) is solved in much the same way. Note that in this case the initial conditions are used $v y = v 0 sinθ$ and $y = 0$ for t=0

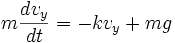$m \frac{dv_y}{dt} = -kv_y+mg$ (2)

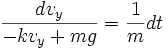$\frac{dv_y}{-kv_y+mg}=\frac{1}{m}dt$ (2a)

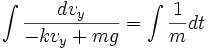$\int{\frac{dv_y}{-kv_y+mg}}=\int{\frac{1}{m}dt}$ (2b)

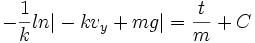$-\frac{1}{k}ln\vert-kv_y+mg\vert=\frac{t}{m}+C$ (2c)

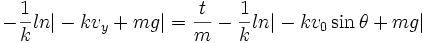$-\frac{1}{k}ln\vert-kv_y+mg\vert=\frac{t}{m}-\frac{1}{k}ln\vert-kv_0 \sin \theta +mg\vert$ (2d) (Substitution of initial values, solved for C, substitution with the result for C)

Having the absolute value function is present in this equation would typically require solving four different cases (multiply the number of possible cases by two for each term in the absolute value signs). However, the absolute value term in the left-hand member is always negative, because the term $- k v y$ can never exceed $m g$ (otherwise air resistance would cause the object to accelerate upward against gravity, this can only happen if the projectile is initially fired with a negative y-component velocity greater than the object's terminal velocity). Because the case where $0^o \le \theta \le 180^o$ is only considered, the right-hand member within the absolute value signs is always negative, since $v 0$ can never exceed $v y$ (and thus $- k v 0$ cannot exceed mg) and $\sin \theta \ge 0$ . Thus, the two terms are combined in the next step, the quotient that appears is always positive, and the absolute value signs can be omitted.

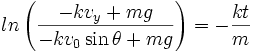$ln\left(\frac{-kv_y+mg}{-kv_0 \sin \theta+mg}\right)=-\frac{kt}{m}$ (2e)

$\frac{-kv_y+mg}{-kv_0 \sin \theta+mg}=e^{-\frac{kt}{m}}$ (2f)

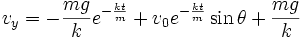$v_y = -\frac{mg}{k}e^{-\frac{kt}{m}}+v_0e^{-\frac{kt}{m}}\sin \theta+\frac{mg}{k}$ (2g)

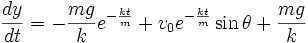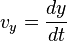$\frac{dy}{dt} = -\frac{mg}{k}e^{-\frac{kt}{m}}+v_0e^{-\frac{kt}{m}}\sin \theta+\frac{mg}{k}$ (2h) (Substitute $v_y = \frac{dy}{dt}$ )

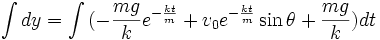$\int{dy}=\int{(-\frac{mg}{k}e^{-\frac{kt}{m}}+v_0e^{-\frac{kt}{m}}\sin \theta+\frac{mg}{k})dt}$ (2i)

$y = \frac{m^2g}{k^2}e^{-\frac{kt}{m}}-\frac{mv_0 \sin \theta}{k}e^{-\frac{kt}{m}}+\frac{mgt}{k}+C$ (2j)

$y =\frac{mv_0\sin\theta}{k}(1-e^{-\frac{kt}{m}})+\frac{m^2g}{k^2}(e^{-\frac{kt}{m}}+\frac{kt}{m}-1)$ (2k) (Substitution of initial values, solved for C, substitution with the result for C, and factorization)

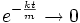The equation for the y-component for velocity (2g), there is a good way of calculating a numerical value for k. If the limit of (2g) is taken as $t\rightarrow\infty$ , results in $e^{-\frac{kt}{m}}\rightarrow 0$ , and all disappears but the 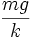$\frac{mg}{k}$ term. $v y$ is also affected by time, but it does not grow indefinitely: the projectile will approach its terminal velocity (in the y direction) as time passes indefinitely, which can be called $v t$ . Using this in (2g) results in:

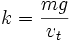
$k = \frac{mg}{v_t}$

Also worth noting is that if the limit as $t\rightarrow\infty$ is taken in equation (1b) there is a maximum value that can be reached by x (if the projectile doesn't hit the ground first). This is given by:

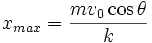
$x_{max}=\frac{mv_0\cos\theta}{k}$

Also, for interest the solutions for $v y$ and $y$ in the case where 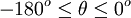$-180^o \le \theta \le 0^o$ are:

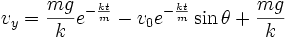
$v_y =\frac{mg}{k}e^{-\frac{kt}{m}}-v_0e^{-\frac{kt}{m}}\sin \theta+\frac{mg}{k}$

$y =\frac{mv_0\sin\theta}{k}(1-e^{-\frac{kt}{m}})+\frac{m^2g}{k^2}(1+\frac{kt}{m}-e^{-\frac{kt}{m}})$ (The solutions for $v x$ and $x$ are not affected.)

An example is given using values for the mass and terminal velocity for a baseball taken from [1].

m = 0.145 kg (5.1 oz)

v₀ = 44.7 m/s (100 mph)

g = -9.81 m/s² (-32.2 ft/s²)

v_t = -33.0 m/s (-73.8 mph)

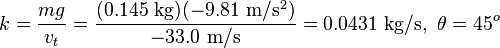$k =\frac{mg}{v_t} = \frac{(0.145 \mbox{ kg})(-9.81 \ \mathrm{m}/\mathrm{s}^2)}{-33.0 \ \mathrm{m}/\mathrm{s}} = 0.0431 \mbox{ kg}/\mbox{s} , \ \theta = 45^o$ .

The red path is the path taken by the projectile modeled by the equations derived above, and the green path is taken by an idealized projectile, one that ignores air resistance altogether. (For those of you who'd prefer those numbers in feet, the conversion factor is 3.28 ft/m) Turns out ignoring air resistance isn't a very good idea (in this case at least): without it a pitcher could throw a home run with 270 ft to spare! (The mechanics of pitching at 45 degrees notwithstanding.) And in some cases it's more accurate to assume $F_a \propto \vec{v}^2$ , meaning when air resistance increases by a factor of p the resistance increases by $p 2$ . In the first example of proportionality, where the velocity was doubled to 8 m/s, the air resistance would instead be quadrupled ( $22 = 4$ ) to 28 N: this only adds to the large amount of error in neglecting air resistance.

[edit] See also

[edit] References

^ "Ballistic trajectory". Defense Technical Information Center. http://www.dtic.mil/doctrine/jel/doddict/data/b/00611.html. Retrieved on 2008-06-10.

[edit] External links

[0] "Ballistic trajectory". Defense Technical Information Center. http://www.dtic.mil/doctrine/jel/doddict/data/b/00611.html. Retrieved on 2008-06-10.

[1]

Trajectory of a projectile

From Wikipedia, the free encyclopedia

Contents

[edit] Notation

[edit] Conditions at the final position of the projectile

[edit] Distance travelled

[edit] Time of flight

`[edit] Angle of reach`

[edit] Conditions at an arbitrary distance `x`

[edit] Height at `x`

[edit] Velocity at `x`

[edit] Derivation

[edit] Angle $θ$ required to hit coordinate (`x`,`y`)

[edit] Trajectory of a projectile with air resistance

[edit] See also

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages

Trajectory of a projectile

From Wikipedia, the free encyclopedia

Contents

[edit] Notation

[edit] Conditions at the final position of the projectile

[edit] Distance travelled

[edit] Time of flight

[edit] Angle of reach

[edit] Conditions at an arbitrary distance x

[edit] Height at x

[edit] Velocity at x

[edit] Derivation

[edit] Angle θ required to hit coordinate (x,y)

[edit] Trajectory of a projectile with air resistance

[edit] See also

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages

`[edit] Angle of reach`

[edit] Conditions at an arbitrary distance `x`

[edit] Height at `x`

[edit] Velocity at `x`

[edit] Angle $θ$ required to hit coordinate (`x`,`y`)