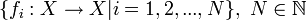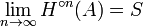Iterated function system

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Sierpinski gasket created using IFS
Colored IFS designed by Chris Ursitti using Apophysis software and rendered by the Electric Sheep.

In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar.

IFS fractals as they are normally called can be of any number of dimensions, but are commonly computed and drawn in 2D. The fractal is made up of the union of several copies of itself, each copy being transformed by a function (hence "function system"). The canonical example is the Sierpinski gasket. The functions are normally contractive which means they bring points closer together and make shapes smaller. Hence the shape of an IFS fractal is made up of several possibly-overlapping smaller copies of itself, each of which is also made up of copies of itself, ad infinitum. This is the source of its self-similar fractal nature.

Contents

[edit] Definition

Formally, an iterated function system is a finite set of contraction mappings on a complete metric space.[1] Symbolically,

\{f_i:X\to X|i=1,2,...,N\},\ N\in\mathbb{N}

is an iterated function system if each fi is a contraction on the complete metric space X.

[edit] Properties

Hutchinson (1981) showed that, for the metric space 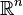\mathbb{R}^n, such a system of functions has a unique compact (closed and bounded) fixed set S. One way of constructing a fixed set is to start with an initial point or set S0 and iterate the actions of the fi, taking Sn+1 to be the union of the image of Sn under the fi ; then taking S to be the closure of the union of the Sn. Symbolically, the unique fixed (nonempty compact) set 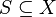S\subseteq X has the property

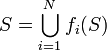S = \bigcup_{i=1}^N f_i(S).

The set S is thus the fixed set of the Hutchinson operator

H(A)=\bigcup_{i=1}^Nf_i(A).

The existence and uniqueness of S is a consequence of the contraction mapping principle as is the fact that

\lim_{n\to\infty}H^{\circ n}(A)=S

for any nonempty compact set A in X. Random elements of S may be obtained by the "chaos game" below.

The collection of functions fi together with composition form a monoid. If there are only two such functions, the monoid can be visualized as a binary tree, where, at each node of the tree, one may compose with the one or the other function (i.e take the left or the right branch). In general, if there are k functions, then one may visualize the monoid as a full k-ary tree, also known as a Cayley tree.

[edit] Constructions

Construction of an IFS by the chaos game

Sometimes each function fi is required to be a linear, or more generally an affine transformation and hence represented by a matrix. However, IFSs may also be built from non-linear functions, including projective transformations and Möbius transformations. The Fractal flame is an example of an IFS with nonlinear functions.

The most common algorithm to compute IFS fractals is called the chaos game. It consists of picking a random point in the plane, then iteratively applying one of the functions chosen at random from the function system and drawing the point. An alternative algorithm is to generate each possible sequence of functions up to a given maximum length, and then to plot the results of applying each of these sequences of functions to an initial point or shape.

Each of these algorithms provides a global construction which generates points distributed across the whole fractal. If a small area of the fractal is being drawn, many of these points will fall outside of the screen boundaries. This makes zooming into an IFS construction normally impractical.

Although the theory of IFS requires each function to be contractive, in practice software that implements IFS only require that the whole system be contractive on average[2].

[edit] Example: a fractal "fern"

Fractal fern using IFS

Here is an example of a fern-like image (Barnsley's fern) computed using an iterated function system.

The first point drawn is at the origin (x0 = 0, y0 = 0) and then the new points are iteratively computed by randomly applying one of the following four coordinate transformations:

1.

xn + 1 = 0
yn + 1 = 0.16 yn.

This coordinate transformation is chosen 1% of the time and maps any point to a point in the line segment shown in green in the figure.

2.

xn + 1 = 0.2 xn − 0.26 yn
yn + 1 = 0.23 xn + 0.22 yn + 1.6.

This coordinate transformation is chosen 7% of the time and maps any point inside the black rectangle to a point inside the red rectangle in the figure.

3.

xn + 1 = −0.15 xn + 0.28 yn
yn + 1 = 0.26 xn + 0.24 yn + 0.44.

This coordinate transformation is chosen 7% of the time and maps any point inside the black rectangle to a point inside the dark blue rectangle in the figure.

4.

xn + 1 = 0.85 xn + 0.04 yn
yn + 1 = −0.04 xn + 0.85 yn + 1.6.

This coordinate transformation is chosen 85% of the time and maps any point inside the black rectangle to a point inside the light blue rectangle in the figure.

The first coordinate transformation draws the stem. The second draws the bottom frond on the left. The third draws the bottom frond on the right. The fourth generates successive copies of the stem and bottom fronds to make the complete fern. The recursive nature of the IFS guarantees that the whole is a larger replica of each frond. Note: The fern is within the range -2.1818 ≤ x ≤ 2.6556 and 0 ≤ y ≤ 9.95851.

[edit] Example

IFS being made with two functions.

The diagram shows the construction on an IFS from two affine functions. The functions are represented by their effect on the bi-unit square (the function transforms the outlined square into the shaded square). The combination of the two functions forms the Hutchinson operator. Three iterations of the operator are shown, and then the final image is of the fixed point, the final fractal.

Early examples of fractals which may be generated by an IFS include the Cantor set, first described in 1884; and de Rham curves, a type of self-similar curve described by Georges de Rham in 1957.

[edit] History

IFS were conceived in their present form by John Hutchinson in 1981 and popularized by Michael Barnsley's book Fractals Everywhere.

[edit] References

  1. ^ Michael Barnsley, "Fractals Everywhere", Academic Press, Inc., 1988.
  2. ^ Draves, Scott; Erik Reckase (July 2007). "The Fractal Flame Algorithm" (pdf). http://flam3.com/flame.pdf. Retrieved on 2008-07-17. 

[edit] See also

Menger sponge, a 3-Dimensional IFS.

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Iterated_function_system"
Personal tools